Algoritmy pro řazení a vyhledávání
Řadící algoritmy
Řadící algoritmus je algoritmus zajišťující seřazení daného souboru dat podle specifického pořadí. Nejčastěji se řadí dle numerické velikosti čísel nebo abecedně.
Z hlediska řazení se vstupní data chápou jako soubor dvojic klíč+hodnota. Po seřazení je posloupnost klíču monotónní, zatímco na připojené hodnoty se nebere zřetel - pouze se přesouvají ze odpovídajícím klíčem.
Algoritmy vnitřního řazení
Vnitřní třídění je takové třídění, kdy předem známe tříděné prvky a máme k dispozici dostatek volné paměti, abychom je uvnitř této paměti mohli setřídit. Opakem je pak třídění vnější, kdy jednotlivé prvky předem neznáme a musíme je ze vstupu postupně načítat v pořadí, v jakém přicházejí. Toto třídění se provádí typicky v situacích, kdy máme operační paměti málo a nejsme schopni v ní všechny prvky uložit. Ve vnějším třídění proto využijeme vnější paměti - pracujeme s jednotlivými soubory na disku. Teoreticky tak můžeme setřídit daleko větší množství dat, operace s vnější pamětí jsou však také podstatně pomalejší. Práce se soubory rychlé algoritmy podstatně degraduje.
Definice problému, který řadící algoritmy řeší:
Na vstupu je posloupnost S = (S1,S2,...,Sn); cílem je najít takovou posloupnost S' = (S'1,S'2,...,S'n), pro kterou platí dvě základní kritéria:
- Tato posloupnost je seřazená: S'1 =< S'2 =< ... =< S'n
- Posloupnost S' je permutací původní posloupnosti S (obsahuje stejná data, jen v jiném pořadí)
V definici relace uspořádání <= se přitom bere ohled poze na klíče příslušných hodnot.
Úloha vnitřního třídění založeného na porovnávání dvou prvků má v nejhorším případě složitost O(n.log n) (to je výborná složitost HeapSortu). Některé algoritmy (QuickSort, nejrychlejší algoritmus v průměrném případě) mohou v ideálním případě dosáhnout i lineární složitosti, jiné zase dosahují složitostí vyšších (O(n2)).
Klasifikace algoritmů
Podle různých kritérií se algoritmy řazení dají dělit do různých skupin. Jak už bylo řečeno, dvě základní skupiny algoritmů jsou tzv. vnitřní a vnější řazení.
Kromě samotných řazených dat také algoritmus zpravidla potřebuje nějakou dodatečnou pracovní paměť. Pokud je velikost této paměti konstantní (nezávislá na množství řazených dat, označováno jako O(1)), algoritmus se označuje jako řazení na původním místě (in situ), jiné algoritmy však potřebují dodatečnou paměť, například místo o velikosti původních dat (tedy O(N) v asymptotickém vyjádření), ve kterém generují seřazený výsledek.
Vstupní data mohou obsahovat několik prvků se shodným klíčem. Podle vzájemné polohy těchto prvků před a po seřazení (kterou lze detekovat podle přidružených dat, která nejsou součástí klíče) se rozlišují tzv. stabilní a nestabilní řadicí algoritmy: stabilní algoritmus zachovává vzájemné pořadí položek se stejným klíčem, u nestabilního není vzájemné pořadí prvků se stejným klíčem zaručeno. (Ale z libovolného nestabilního algoritmu lze učinit stabilní tím, že se klíč každé položky vstupních dat rozšíří o pozici položky v původním souboru.)
Podle chování na částečně seřazených souborech dat se rozlišují algoritmy přirozené a nepřirozené: přirozený algoritmus rychleji zpracuje seřazenou množinu než neseřazenou.
Dále lze algoritmy zhruba rozdělit podle základní myšlenky. Existuje několik základních druhů algoritmů univerzální vnitřního řazení, přičemž některé pokročilejší algoritmy kombinují více postupů. Např.:
-
Řazení výběrem: V souboru se vždy najde nejmenší ze zbývajících
položek a uloží na konec postupně budovaného seřazeného souboru.Ukázka řazení Výběr Vkládaní Záměna 614532 1*64532 6?14532 145326 12*6453 16?4532 143256 123*645 146?532 132456 1234*65 1456?32 123456 12345*6 13456?2 123456 -
Řazení vkládáním: Ze souboru neseřazených dat se postupně bere položka po položce a vkládá se na správné místo v seřazeném souboru (zpočátku prázdném).
-
Řazení slučováním: Vstupní soubor se rozdělí na části, které se (typicky rekurzivně) seřadí; výsledné seřazené části se poté sloučí takovým způsobem, aby i výsledek byl seřazený.
Neexistuje žádný dokonalý řadicí algoritmus, který by byl ideální pro všechna použití. Různé algoritmy mají různé vlastnosti co se týká jejich očekávané časové a paměťové složitosti, náročnosti implementace a dalších vlastností. Pro konkrétní podmínky se tak často navrhují specifické varianty.
Běžné algoritmy
|
Přehled běžných univerzálních algoritmů řazení |
||||||||
|
Název |
Časová složitost |
Dodatečná paměť |
Stabilní |
Přirozená |
Metoda |
|||
|
Anglicky |
Česky |
Minimum |
Průměrně |
Maximum |
||||
|
Bublinkové řazení |
O( n ) |
O(n2) |
O(n2) |
O(1) |
ano |
ano |
záměna |
|
|
Řazení haldou |
O(n log n) |
O(n log n) |
O(n log n) |
O(1) |
ne |
ne |
|
|
|
Řazení vkládáním |
O( n ) |
O(n2) |
O(n2) |
O(1) |
ano |
ano |
vkládání |
|
|
Řazení slučováním |
O(n log n) |
O(n log n) |
O(n log n) |
O(1) |
ano |
ano |
slučování |
|
|
Rychlé řazení |
O(n log n) |
O(n log n) |
O(n2) |
O(log n) |
ne |
ne |
záměna |
|
|
Řazení výběrem |
O(n2) |
O(n2) |
O(n2) |
O(1) |
ano |
ano |
výběr |
|
|
Shellovo řazení |
|
|
O(n log n) |
O(1) |
ne |
ano |
vkládání |
|
Dobré příklady řadících algoritmů s vizualizací najdete tady
Bubble sort
Bubble sort je způsob řazení kdy algoritmus opakovaně prochází seznam, přičemž porovnává každé dva sousedící prvky, a pokud nejsou ve správném pořadí, prohodí je (menší, větší). Porovnávání prvků běží do té doby, dokud není seznam seřazený. Pro praktické účely je neefektivní, využívá se hlavně pro výukové účely či v nenáročných aplikacích.
Algoritmus je univerzální (pracuje na základě porovnávání dvojic prvků), pracuje lokálně (nevyžaduje pomocnou paměť), je stabilní , patří mezi přirozené řadicí algoritmy (částečně seřazený seznam zpracuje rychleji než neseřazený).
Pracuje opakovaným přechodem přes seznam, přičemž porovnává dva sousedící prvky, a pokud nejsou ve správném pořadí, prohodí je. Porovnávání prvků běží do té doby, dokud není seznam seřazený (tj. neprovedla-li se při průchodu posloupností mžádná změna). Složitost algoritmu je O(n2).
Postup v krocích:
-
Posloupnost rozdělíme na 2 čáasti, setříděnou a nesetříděnou. Setříděná část je prázdná.
-
Postupně porovnáme všechny sousední prvky v nesetříděné části, a pokud nejsou v požadovaném pořadí, prohodíme je.
-
Krok 2 opakujeme tak dlouho, dokud nesetříděná část obsahuje více než 1 prvek. Jinak algoritmus končí.
Insert sort (řazení s přímým vkládáním)
Pole se rozdělí na setříděnou (od indexu 0 do i - 1) a nesetříděnou část (od indexu i do n - 1, kde n je počet prvků pole). Z nesetříděné části vybereme libovolný prvek a ten zařadíme do setříděné části tak, aby zůstala setříděná. Tento postup opakujeme, dokud není nesetříděná část prázdná.
Nalezne-li se index k (0 =< k =< i), pro nějž platí pole[k-1] =< pole[i] =< pole[k], pak se část od indexu k do i-1 posune o jednu pozici doprava a na uvolněnou pozici k se vloží zařazovaná položka s indexem i.
Inicializace spočívá v rozdělení pole na dvě části. Prvek pole[0] tvoří setříděnou část a zbytek pole nesetříděnou část. Cyklus končí zařazením posledního (n-tého) prvku. Složitost algoritmu je O(n2).
Popis v krocích:
- První prvek pole ponecháme na svém místě.
- Vezmeme druhý prvek a porovnáme jej s prvním. Je-li menší, zařadíme ho na první místo a první prvek posuneme, jinak je ponecháme na místě.
- Vezmeme třetí prvek a porovnáme jej s prvními dvěma prvky. Je-li menší než některý z nich, zařadíme jej na odpovídající pozici a následující prvky podle potřeby posuneme. Jinak je ponecháme na původních místech.
- Obdobně postupujeme i s ostatními prvky v poli.
Merge sort (řazení slučováním)
Algoritmus řazení slučováním je opakem algoritmu řazení dělením. Místo dělení posloupnosti se u tohoto algoritmu slučují seřazené podposloupnosti.
Naším úkolem je seřadit prvky jednoho pole. Předpokládejme, že v poli pole jsou dva seřazené úseky. Seřadit je algoritmem řazení slučováním můžeme tak, že vytvoříme pole pom s bitonickou posloupností prvků pole pole, tj. druhý úsek bude seřazen sestupně. Složitost algoritmu je O(n log n)).
Popis v krocích:
- Rozdělí neseřazenou množinu dat na dvě podmnožiny o přibližně stejné velikosti
- Seřadí obě podmnožiny
- Spojí seřazené podmnožiny do jedné seřazené množiny
Select sort
Principem tohoto řazení je výběr mezního prvku (maximum nebo minimum) z tříděné posloupnosti a jeho záměna s prvním (posledním) prvkem. V dalším kroku máme pole o (n-1) prvcích a opakujeme totéž. Takto postupujeme až do úplného seřazení posloupnosti. Získaná posloupnost bude seřazená vzestupně v případě, že budeme vybírat z nesetříděné posloupnosti nejmenší prvek a zařadíme ho na začátek posloupnosti, a sestupně v případě, že vybereme největší prvek z nesetříděné posloupnosti a zařadíme ho na začátek. Při tomto řazení se vlastně setříděná část pole postupně zvětšuje a nesetříděná část naopak zmenšuje. Algoritmus končí v případě, že nesetříděná část již neobsahuje žádný prvek. Tato metoda je vnitřní, přímá a jednoduchá. Nevýhodou tohoto algoritmu je, že jestliže se na vstupu nachází již částečně setříděná posloupnost, algoritmus to nerozlišuje a proběhne v maximálním počtu koků. Složitost algoritmu je O(n2)
Popis v krocích:
-
V posloupnosti najdeme nejmenší prvek a vyměníme ho s prvkem na první pozici. Tím dojde k rozdělení posloupnosti na dvě části. Setříděná část obsahuje pouze jeden prvek, nesetříděná n-1.
- Obsahuje-li nesetříděná část více než jeden prvek, pokračujeme bodem 2, jinak je třídění ukončeno.
- V nesetříděné části najdeme nejmenší prvek a vyměníme ho s prvním prvkem v nesetříděné části, čímž dojde k zařazení tohoto prvku do setříděné části.
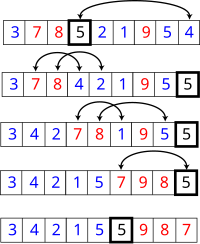
Shell sort
Algoritmus řazení ShellSort vychází z algoritmu řazení vkládáním (InsertSort), je ale mnohem ekonomičtější. Klasické řazení vkládáním je totiž poměrně pomalé, když prvky v řazené posloupnosti jsou vzdálené od své správné pozice v seřazené posloupnosti, protože jsou vyměňovány jenom se svým sousedem.
Např. budeme mít posloupnost prvků: 4, 2, 7, 6, 3, 9, 8, 5, 1, 0
Vložíme-li postupně prvky 2, 7, ...., 5 na správná místa dostaneme posloupnost 2, 3, 4, 5, 6, 7, 8, 9, 1, 0.
Prvky 0 a 1 musí pro dosažení správné pozice projít téměř celou posloupnost, což je pomalé.
Aby se zkrátila cesta prvku na správnou pozici, seřadíme vkládáním prvky vzdálené H. Celá řazená posloupnost je nyní organizována jako H podposloupností začínajících na pozicích 0, 1, ..., H-1, každá obsahující prvky vzdálené H.
Pro posloupnost prvků: 4, 2, 7, 6, 3, 9, 8, 5, 1, 0 a H = 4 je situace následující:
| 4 | 2 | 7 | 6 | 3 | 9 | 8 | 5 | 1 | 0 |
| 4 | 2 | 7 | 6 | 3 | 9 | 8 | 5 | 1 | 0 |
| 4 | 2 | 7 | 6 | 3 | 9 | 8 | 5 | 1 | 0 |
| 4 | 2 | 7 | 6 | 3 | 9 | 8 | 5 | 1 | 0 |
Apliujeme-li na tyto posloupnosti algoritmus řazení vkládáním, cesta prvků 0 a 1 k jejich správné pozici se podstatně zkrátí.
Uvedeme si jednotlivé kroky, přičemž prvky, které vkládáme na správnou pozici podtrhneme:
| 3 | 2 | 7 | 6 | 4 | 9 | 8 | 5 | 1 | 0 |
| 1 | 2 | 7 | 6 | 3 | 9 | 8 | 5 | 4 | 0 |
| 1 | 2 | 7 | 6 | 3 | 9 | 8 | 5 | 4 | 0 |
| 1 | 0 | 7 | 6 | 3 | 2 | 8 | 5 | 4 | 9 |
| 1 | 0 | 7 | 6 | 3 | 2 | 8 | 5 | 4 | 9 |
| 1 | 0 | 7 | 5 | 3 | 2 | 8 | 6 | 4 | 9 |
Obecně po seřazení všech podposloupností s prvky vzdálenými H získáme posloupnost, které říkáme, že je H seřazena. V našem příkladě je poslední posloupnost 4 seřazena.
Volbou dostatečně velkého H vzhledem k počtu řazených prvků, tak můžeme posunout prvky posloupnosti na velkou vzdálenost. Dále postup opakujeme pro klesající posloupnost hodnot H. Je-li poslední hodnota 1 získáme seřazenou posloupnost.
Jaká má být posloupnost hodnot H. Shell navrhl pro posloupnost s N prvky začít s N/2 a postupně tuto hodnotu půlit dokud nedosáhne 1. Vzdálenost mezi řazenými prvky klesá geometricky, tedy jejich počet je log2N. Na druhé straně v tomto případě prvky na sudých pozicích nejsou porovnány s prvky na lichých pozicích až do posledního průchodu.
Knuth navrhl zvolit počáteční vzdálenost přibližně třetinovou a postupně ji dělit třemi. Přesněji, posloupnost vzdáleností jsou prvky posloupnosti 1, 4, 13, 40, 121, 364, 1093, 3280, ..., což jsou čísla tvaru 3i + 1, i = 0, 1, ... .
PF sort (řazení prioritní frontou)
Princip řazení prioritní frontou spočívá ve vybírání maximálního nebo minimálního prvku, který je následně vkládán od konce původního pole. Tím získáme vzestupně nebo sestupně uspořádané pole.
Popis v krocích:
- Prvky neuspořádaného pole uložíme postupně do prioritní fronty.
- Nyní z fronty vybereme největší (nejmenší) prvek, který uložíme na konec původního pole.
- Opět vybereme největší (nejmenší) prvek, který uložíme na místo o jednu pozici menší než předchozí prvek.
- Krok 3 opakujeme, dokud není fronta prázdná.
Pro toto řazení můžeme použít prioritní frontu realizovanou pomocí pole, spojového seznamu nebo stromu. Z tohoto typu řazení pak vychází řazení haldou.
Příklad :
Setřídíme algoritmem SelectSort posloupnost prvků 15, 4, 28, 9, 51, 21, 14.
Vzestupné třídění:
|
15 |
4 |
28 |
9 |
51 |
21 |
14 |
|
|
|
|
|
|
|
51 |
|
|
|
|
|
|
28 |
51 |
|
|
|
|
|
21 |
28 |
51 |
|
|
|
|
15 |
21 |
28 |
51 |
|
|
|
14 |
15 |
21 |
28 |
51 |
|
|
9 |
14 |
15 |
21 |
28 |
51 |
|
4 |
9 |
14 |
15 |
21 |
28 |
51 |
První řádek odpovídá prioritní frontě. Ostatní řádky představují, jak se zaplňuje tříděné pole maximálními prvky vybíranými z prioritní fronty.
Sestupné třídění:
|
15 |
4 |
28 |
9 |
51 |
21 |
14 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
9 |
4 |
|
|
|
|
|
14 |
9 |
4 |
|
|
|
|
15 |
14 |
9 |
4 |
|
|
|
21 |
15 |
14 |
9 |
4 |
|
|
28 |
21 |
15 |
14 |
9 |
4 |
|
51 |
28 |
21 |
15 |
14 |
9 |
4 |
První řádek odpovídá prioritní frontě. Ostatní řádky představují, jak se zaplňuje tříděné pole minimálními prvky vybíranými z prioritní fronty.
Složitost algoritmu je O(n log n).
Heap sort
Toto řazení je podobné jako předchozí řazení prioritní frontou s tím rozdílem, že prioritní fronta je realizována haldou. Potom při výběru největšího (nejmenšího) prvku z kořene haldy nastává obnova haldy, která může znamenat cestu až k listům délky log2n. Poslední cesta bude mít délku log21 a tedy časová náročnost řazení je menší než n log2n:
log2n + log2(n - 1) + ... + log22 + log21 < n log2n
Řazení výběrem mezního prvku (SelectSort, PFSort) je založeno na nalezení největšího (nejmenšího) prvku postupným procházením nesetříděné části. Metoda řazení pole haldou pracuje podobně s tím, že výběr největšího prvku z neseřazené části je efektivnější. Neprochází totiž všechny ještě neseřazené prvky, ale protože tyto jsou organizovány v haldě, pro obnovu vlastnosti haldy po odebrání největšího (nejmenšího) prvku nutno projít nejvíce log2(pocet neseřazených prvků).
Popis v krocích:
- Po načtení všech prvků, budeme procházet polem od jeho začátku metodou
nahoru()a vlevo od okamžité pozice budeme vytvářet haldu (je to fáze vytvoření haldy). Prvky řazeného pole v uvedené implementaci jsou uloženy vpole[1]ažpole[pocet]. - Následuje fáze řazení, kdy vyměníme kořen haldy (první prvek pole s posledním prvkem haldy a v poli obnovíme metodou
dolu()haldu zmenšenou o jeden prvek. - Krok 2 opakujeme tak dlouho, dokud není pole seřazeno.
Quick sort (třídění rozdělováním)
Quicksort je jeden z nejrychlejších známých algoritmů řazení založených na porovnávání prvků. Jeho průměrná časová složitost je pro algoritmy této skupiny nejlepší možná (O(n log n)), v nejhorším případě (kterému se ale v praxi jde obvykle vyhnout) je však jeho časová náročnost O(n2). Další výhodou algoritmu je jeho jednoduchost.
Základní myšlenkou quicksortu je rozdělení řazené posloupnosti čísel na dvě přibližně stejné části (quicksort patří mezi algoritmy typu rozděl a panuj). V jedné části jsou čísla větší a ve druhé menší, než nějaká zvolená hodnota (nazývaná pivot). Pokud je tato hodnota zvolena dobře, jsou obě části přibližně stejně velké. Pokud budou obě části samostatně seřazeny, je seřazené i celé pole. Obě části se pak rekurzivně řadí stejným postupem.
Obecně postupujeme tak, že projdeme pole zleva dokud nenalezneme větší prvek než dělící prvek v a dále ho projdeme zprava, dokud nenalezneme menší prvek než dělící prvek. Tyto prvky pak vyměníme.
Největším problémem celého algoritmu je volba pivota. Pokud se daří volit číslo blízké mediánu řazené části pole, je algoritmus skutečně velmi rychlý. V opačném případě se jeho časová složitost blíží O(N2). Přirozenou metodou na získání pivota se pak jeví volit za pivot medián. Hledání mediánu (a obecně k-tého prvku) v posloupnosti běží v lineárním čase k počtu prvků, tím dostaneme složitost O(Nlog2N) v nejhorším případě. Nicméně tato implementace není příliš rychlá z důvodu vysokých konstant schovaných v O notaci. Proto existuje velké množství alternativních způsobů, které se snaží efektivně vybrat pivota co nejbližšího mediánu. Zde je seznam některých metod:
-
První prvek - popřípadě kterákoli jiná fixní pozice. Velmi nevýkonná především na částečně seřazených množinách.
-
Náhodný prvek - často používaná metoda. Lze dokázat, že pokud je pozice pivotu skutečně náhodná, algoritmus poběží v O(N log N)). Skutečně náhodná čísla generují ale pouze hardwarové generátory, které nemusí dodávat data dostatečně rychle. V praxi mnohdy stačí použít pseudonáhodný algoritmus.
-
Metoda mediánu tří - případně pěti, či libovolné jiné konstanty. Pomocí pseudonáhodného algoritmu (používají se i fixní pozice) se vybere X prvků z množiny, ze kterých se použitím některého primitivního řadícího algoritmu najde medián a ten je zvolen za pivota.
Přestože Quicksort nemá zaručenou časovou složitost O(n log2 n)), reálné aplikace a testy ukazují, že na pseudonáhodných datech je vůbec nejrychlejší ze všech obecných řadících algoritmů (tedy i rychlejší než Heapsort a Mergesort, které jsou formálně rychlejší). Maximální časová náročnost O(n2) ho však diskvalifikuje pro použití v kritických aplikacích.